原理介绍
Divide and Conquer:分治算法,分而治之。山高皇帝远,治理国家,不可能所有的事情都由皇帝解决,国家分省、市、县、镇、村,层层管理,最终汇总合并到皇帝。借鉴于这种思想,将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且与原问题相同(如果子问题的规模仍然不够小,则再继续划分),然后递归求解这些问题,最好用适当的方法将各子问题的解合并成原问题的解。
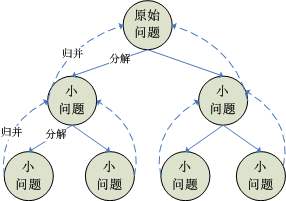
解题步骤
分解
将要解决的问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题。
治理
求解各个子问题,由于子问题的形式与原问题相同,只是规模较小而已,而当子问题划分得足够小时,就可以用简单得方法解决。
合并
按照原问题的要求,将各个子问题的解逐层合并,构成原问题的解。
经典例题(合并排序)
问题描述
给定一个无序数列,将其排成有序数列。
第一行输出元素的个数n,第二行依次输出数列中的元素(用空格分开)
1 | 8 # 元素的个数 |
算法分析
在数列排序中,数越少越容易排序,基于这个思想,可以考虑将长序列分成短序列,当序列分为只有一个元素时,其本身即为有序。
然后执行合并操作,将两个有序序列合并为一个有序序列也是较为容易的。
归并图解

python代码实战
1 | import sys |
代码运行结果

经典例题(快速排序)
问题描述
给定一个无序数列,将其排成有序数列。
第一行输出元素的个数n,第二行依次输出数列中的元素(用空格分开)
1 | 9 # 元素的个数 |
算法分析
快速排序的思想和合并排序类似,都是采用分治算法,区别之处在于,合并排序通过先分裂,再合并,合并的同时进行排序。而快速排序是先进行排序,生成两段有序的数列,然后找到分裂点再进行分裂,最后再合并。
如何找到分裂点是快速排序的难点
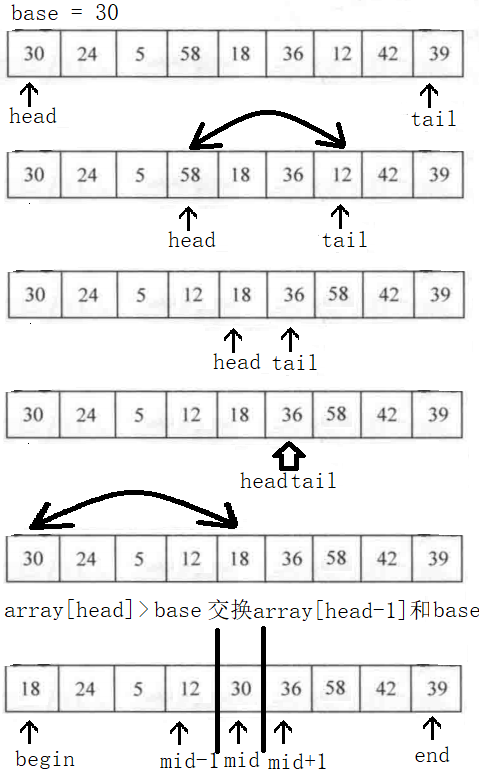
(1)首先取数组的第一个元素作为基准元素base,建立一个头指针和一个尾指针。
(2)从左向右进行扫描,如果找到大于base的元素,头指针停留在此处,进入步骤(3)。
(3)从右向左进行扫描,如果找到小于等于base的元素,尾指针停留在此处,然后交换头尾指针的值,并且头指针向右移动一个距离,尾指针向左移动一个距离。
(4)重复(2)和(3),直到头指针大于等于尾指针的位置。此时头指针之前的元素都是小于等于基准元素的,头指针之后的元素都是大于基准元素的。
找到分裂点以后,根据分裂点将长数列分解成短数列重复上述方法进行分裂,最终将分裂的结果按顺序合并即可。
快排图解
python代码实战
1 | import sys |
代码运行结果

经典例题(大数乘法)
问题描述
现有两个很大的数据,由于计算机硬件的限制,无法用乘法直接进行求解,如何设计算法求解出正确的结果?
第一行输入乘数a,第二行输入乘数b
1 | 1122334455667788998877665544332211 #乘数 a |
算法分析
由于计算机的硬件限制,无法对大值数据进行操作,因此需要根据运算的法则对数据进行分解。
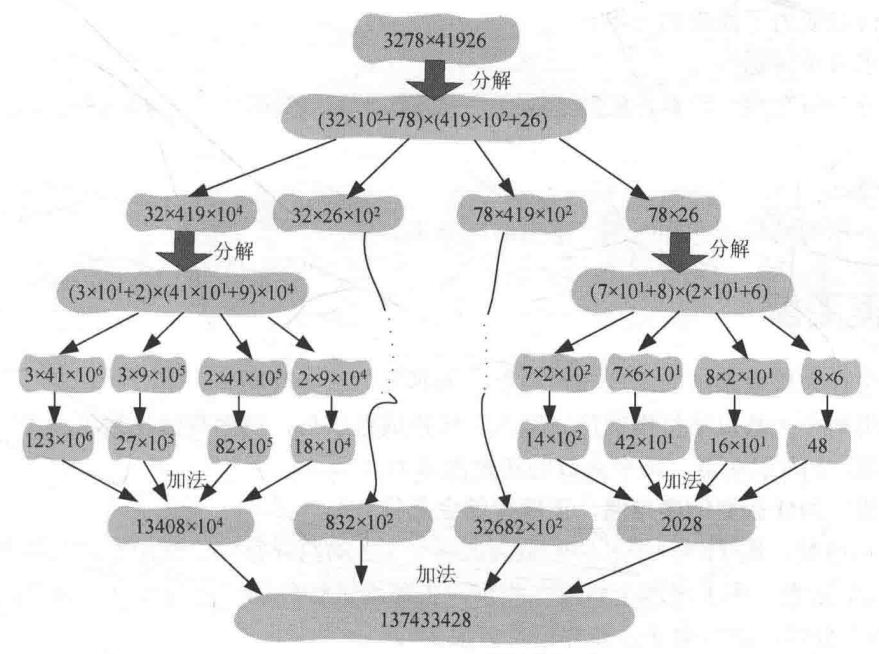
假设要计算$3278 * 41926$,可以将两个数进行分解,将3278分解为$(32*10^2)+(78*10^0)$,将41926分解为$(419*10^2)+(26*10^0)$,然后根据乘法的运算性质$(a+b)*(c+d)=ac+ad+bc+bd$可得原式为$(32*419*10^4)+(32*26*10^2)+(78*419*10^2)+(78*26*10^0)$。
然后发现上式的第一项$(32*419*10^4)$还可以进行分解,将32分解为$(3*10^1)+(2*10^0)$,将419分解为$(41*10^1)+(9*10^0)$,……,直到分解出的两个数中有一个为一位数则不需要分解,因为一位数的乘法很简单。
乘法图解
python代码实战
1 | import sys |
代码运行结果

算法总结
分治算法的难点是如何进行分解,就像盗梦空间的梦境一样,层层深入,却要清醒在每一层应该做什么事情。是应该先分裂再做事情还是先做事情在分裂也是需要考虑的。最重要的一点是梦境不能永远深入,一定要在某一个时机回到现实,即要拥有截止条件,判断是否已经达到需要的深度。